Image Segmentation

A Scikit-based implementation of the Random Walker Algorithm for image segmentation - distinuishing various features in digital images.

GitHub Repository

ksheersagaragrawal/Image-Segmentation-using-Random-Walker-Algorithm ksheersagaragrawal/Image-Segmentation-using-Random-Walker-Algorithm

Keywords

Image Segmentation, Random Walker Algorithm, Graph Theory, Digital Image Processing, Python, Numpy, AI in Imaging, Computational Techniques.

Random Walk Algorithm Formulas

The Random Walk Algorithm for image segmentation is based on the following steps and formulas:

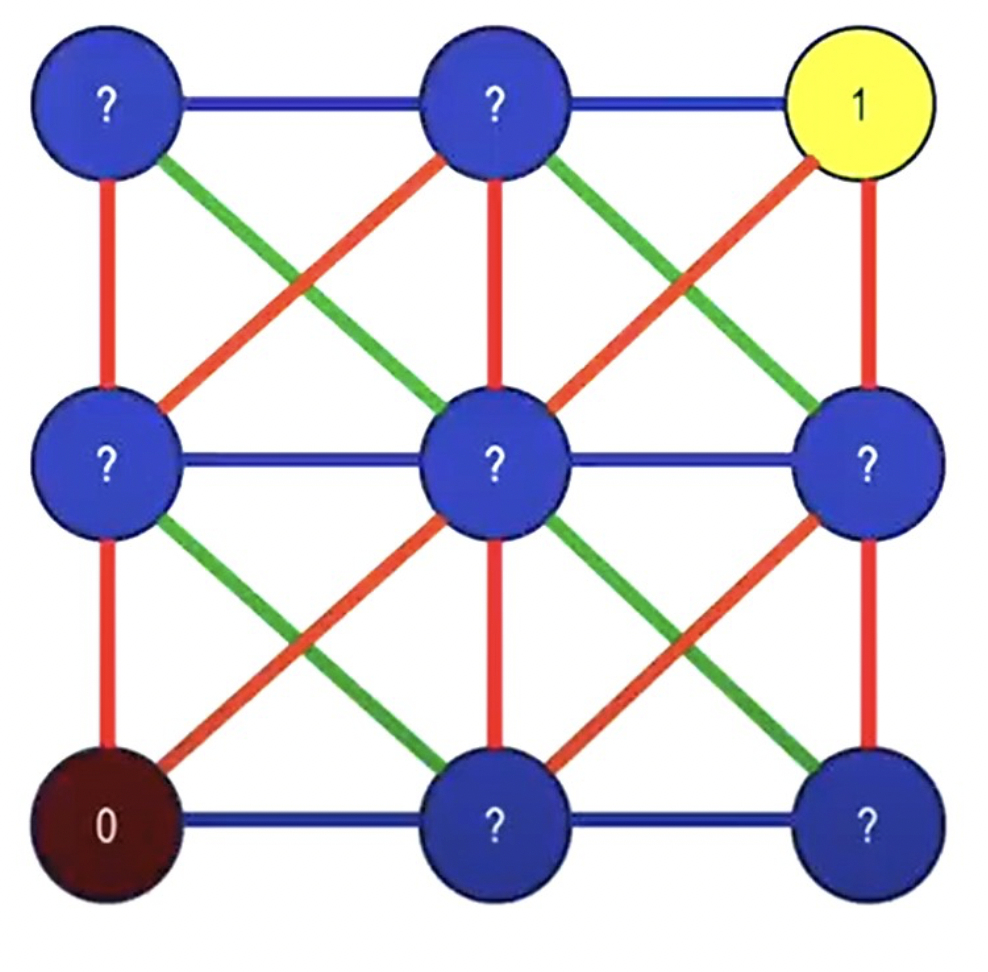
  1. Node Marking: The nodes in the image are marked based on the following criteria:
    • Let p(i, j) be the pixel value at position (i, j) in the image.
    • Mark the nodes as follows:
      • If p(i, j) > 110, then mark as 255 (white).
      • If p(i, j) < 75, then mark as 0 (black).

  2. Matrix Operations: All the unmarked nodes will be marked in subsequent steps. The key formula in the Random Walk Algorithm for image segmentation is:

    \[L_u \cdot X = (-B)^T \cdot M\]

    Where:

    • \(L_u\) is a submatrix of the L matrix containing information about all the unmarked to unmarked nodes.
    • \(X\) is the matrix representing probabilities.
    • \(B^T\) is a submatrix of the L matrix that contains information about all the unmarked nodes to marked nodes.
    • \(M\) matrix is defined for zero and 255 class \(M_0\) and \(M_{255}\).
  3. Calculating Probabilities:

    • First, calculate \(X\) using the formula: \(X = L^{-1} \cdot (B^T) \cdot M\) where \(L^{-1}\) is the inverse of matrix \(L\), \(B^T\) is the transpose of matrix \(B\), and \(M\) is the predefined matrix.

    • The probability for pixel \(k\) taking the value 0 is given by the corresponding element in matrix \(X\) for \(M_0\), which can be represented as: \(P(k \text{ takes value } 0) = X_k \text{ for } M_0\) where \(X_k\) is the k-th element in the matrix \(X\).

  4. Image Construction:
    • Construct a new image from \(X\) by comparing their probability to determine the final pixel values.
Pixels represent nodes with directed, weighted edges.

Accuracy Calculation

The accuracy of the segmentation is calculated as follows:

\[\text{Accuracy} = \frac{|\text{White Pixels in SkitLearn} - \text{White Pixels in New Image}|}{\text{Total White Pixels} + \text{Total Black Pixels}}\]

Collab File